Regular tessellations in OpenGL Shader Language
Tiles

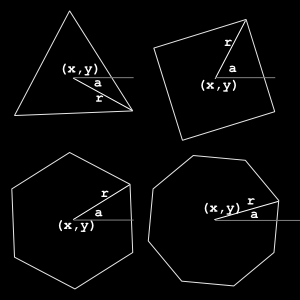
I wanted to create a tiling of regular polygons in GLSL. I was particularly interested in (equilateral) triangles, but also wanted to explore hexagons, squares, and octagons. One goal was to create a 'tile' data structure that would let me separate the tessellation code from the rendering code.
The tile data structure stores the center point, the radius, the number of sides, and the rotation angle. This is sufficient to calculate most aspects from a polygon (eg, distance to the center, distance to a vertex, distance to an edge).
The tile structure also stores the inner radius (the radius to the closest point of the edge), the side length, a direction flag (indicating clockwise or counter clockwise progression of the vertices), and a 'horizontal offset angle'. The horz-angle is the angle between vertex 0 of a canonical polygon and horizontal (0 degrees).
struct Tile_t
{
vec2 center; // Center of the tile
int sides; // Number of sides
float len; // Length of the side
float radius; // Radius to the vertex
float inner; // Radius to closest point on the edge
float angle; // Angle to first vertex
float horzangle; // Angle between canonical first vertex and horizontal
int direction; // Rotation direction (+1 or -1)
};
Mapping a coordinate to a polygon.
To map a coord to a tile we divide the 2D coordinate space into one or more overlapping rectangular grid, determine which grid rects contain the coordinate, and, if more than one rect is found, select the appropriate rect and generate the tile.
For squares we only need one grid to find each polygon, i.e., square. For all other tessellations we need two grids.
Squares
For squares, the grid spacing is the same in both directions and equals the length of the side of the square. Since the tessellation parameter is specified as the polygon radius, the length is computed as len=radius*sqrt(2). To find which square the coord is in we divide coord.x by the grid width, floor() this, and multiply back by the grid width. We do the same for coord.y. This gives the lower left corner of the square. Next we add a "center offset" (sidelen/2, sidelen/2) to get to the center of the square. Be design we specify that vertex zero is top right, which means that the angle is set to 45 degrees.
Triangles
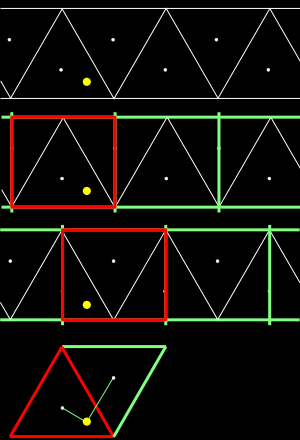
For (equilateral) triangles the two grids are the same size, but offset horizontally from each other by 1/2 the length of a side. The width of the grid is the length of one side. The height is cos(30)*length. If you look at one row of triangles you can see that the first grid aligns with bases of the triangles pointing up. For these triangles the center offset is (len/2, rad/2). For the triangles pointing down the center offset is (len/2, rad). With each grid we find the grid rect that contains the point. We will always find a rect in each grid. The next step is to determine which rect should be selected, that is, which triangle contains the point. We do this by calculating the distance from the coordinate to each polygon center and select the grid with that had the center closer to the coordinate. Note that for alternating rows the triangles alternate their orientation, so the calculation for the center needs to take into account if it is an even or odd row.
Hexagons
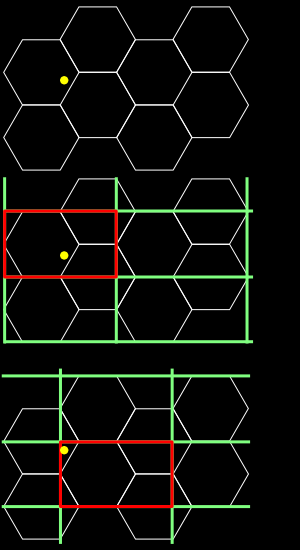
For hexagons, the second grid is offset both horizontally and vertically. Also both grids have an area that does not include a hexagon. This means that even though a grid rectangle is located it maybe discarded. Therefore, if only one rect is found them that is the polygon, but if two are found then a similar decision is used as with triangles.
Octagons
Locating the octagons is similar to squares, but two grids are required. The second grid is used to locate the small squares.
Rotation and Direction: Style Variations in a Tessellation
(creating "seamless" tiling)
